[STL] 히프 heap와 트리 자료구조

stl에서 제공하는 계층형 컨테이너 중 하나인 map과 heap은 트리라는 자료구조의 형태로 구현되어 있습니다. 따라서 오늘은 STL map과 heap에 대해 알아보기 전에 트리 자료구조에 대하여 알아보겠습니다.

트리$($Tree)

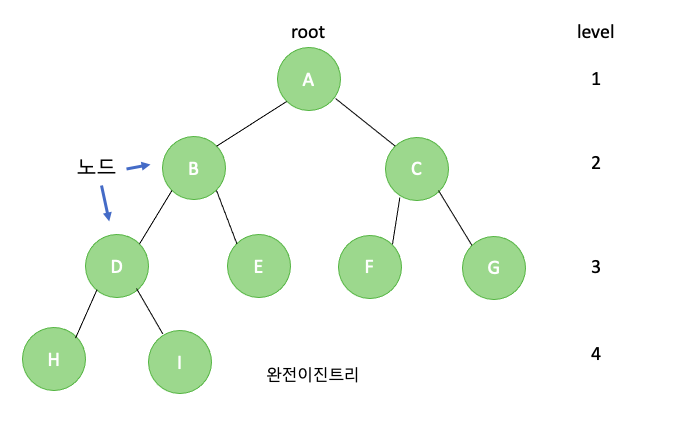
• 노드의 차수 : 해당 노드의 서브 트리의 수
  ex$)$ 노드 D의 차수 = 3
• 트리의 차수 : 트리에 포함된 노드들 중의 최대 차수.
  ex$)$ 이진 트리의 최대 차수 = 2
• 단말노드 : 차수가 0인 노드.
  ex$)$ 노드 E, F, G…
• 레벨 : 루트의 레벨이 1일 때 부모-자식은 1레벨씩 증가
  
• 트리의 높이 : 트리에 속한 노드의 최대 레벨. $($위의 완전이진트리의 경우 높이=4)

트리란 위와 같이 노드의 부모, 자식관계를 이용하여 트리구조로 대량의 데이터를 저장하는 형태를 말합니다. 이러한 트리중 각 노드의 최대 차수가 2인 트리를 이진트리 라고 하며 이진트리중에서도 마지막 전 레벨까지 트리가 꽉차있고 왼쪽부터 채워지는 트리를 완전이진트리라고 합니다. 완전이진트리인 경우 1차원 배열을 사용하여 데이터를 저장하고 아니라면 리스트를 사용하여 데이터를 저장하게 됩니다.

완전이진트리인 경우의 일차원 배열 표현

n개의 노드를 가진 완전이진트리를 아래의 공식을 통해 일차원 배열에 저장하게 됩니다. $($i = index)

• parent$($i) = i/2 의 위치 $($i ≠ 1)
• leftChild$($) = 2i 의 위치 $($2i ≤ n)
• rightChild$($) = 2i+1 의 위치 $($2i+1 ≤ n)
• 첨자 0의 위치는 사용되지 않음

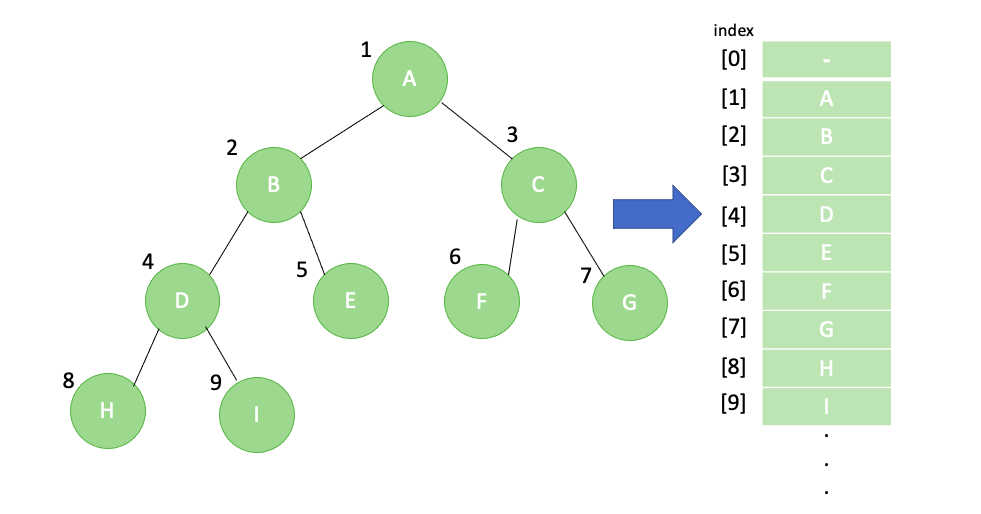
이와같이 트리를 일차원 배열에 저장하는 경우는 간편 하지만 완전이진트리가 아닌 경우엔 많은 메모리가 낭비될 수 있다는 단점이 있습니다. 따라서 완전이진트리가 아닌경우엔 링크 표현을 사용하여 트리를 저장합니다.

완전이진트리가 아닌 경우의 링크 표현

링크표현에서 하나의 노드는 자식 노드를 가리키는 두개의 포인터와 하나의 데이터 필드로 이루어져 있습니다.

|leftChild|data|rightChild| |-|-|-| 앞에서 다루었던 완전이진 트리를 링크를 사용하여 표현하면 다음과 같이 나타낼 수 있습니다.

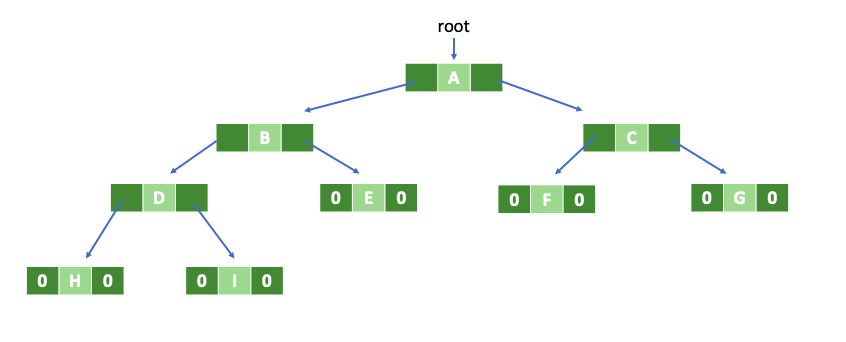
초기의 root 포인터는 널값을 가리키고 있지만 트리가 생성되면 root 노드의 주소를 갖게됩니다.

이진 트리 순회

트리의 각 노드에 한 번씩 방문하는 방법으로 전위(preorder), 중위(inorder), 후위(postorder) 순회가 있습니다. 각 방법의 순회 순서는 다음과 같습니다.

• preorder : root, left subtree, right subtree 순
• inorder : left subtree, root, right subtree 순
• postorder : left subtree, right subtree, root 순

ex$)$

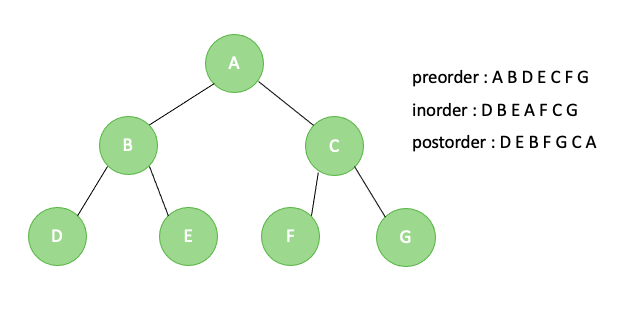
히프 $($Heap)

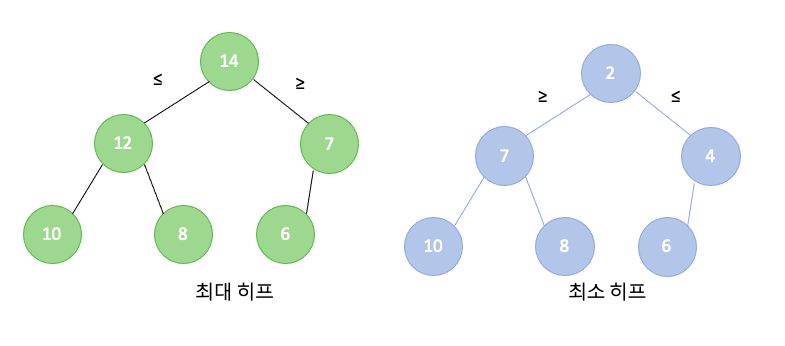
• 최대 트리 : 부모의 키값 ≥ 자식의 키값
• 최소 트리 : 부모의 키값 ≤ 자식의 키값
• 최대 히프 : 최대 트리이며 완전 이진 트리
• 최소 히프 : 최소 트리이며 완전 이진 트리

최대 히프에서의 삽입 최대 히프에서 값을 삽입할때 최대 히프의 조건을 만족시켜야 하기 때문에 완전 이진 트리의 맨 아래 남은 위치를 잠정적 위치로 놓고 부모노드와 값을 비교해 나갑니다.

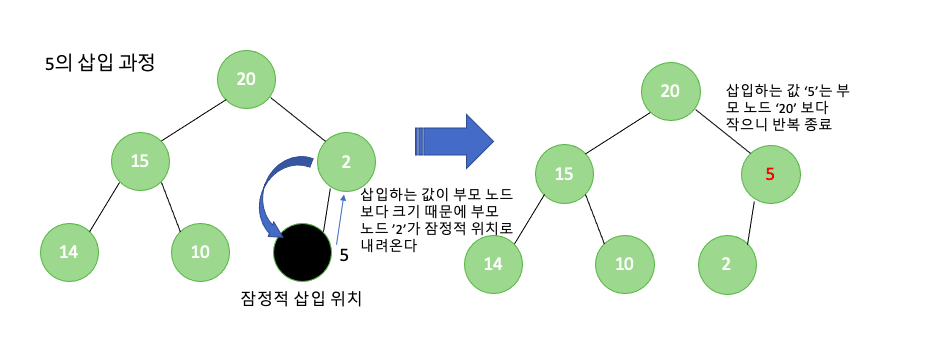
만약 부모노드의 값보다 삽입한 값이 더 크면 부모노드는 잠정적 위치로 내려오게 됩니다. 이와 같은 작업을 삽입한 값보다 부모가 더 크거나 부모가 널값인 경우 까지 반복합니다.

삽입의 경우 최대 완전 이진 트리의 높이 만큼 반복하게 되며 완전 이진 트리의 높이는 노드가 n개 일때 [log2(n+1)] 이므로 시간복잡도는 O(log2n) 이됩니다.

최대 히프에서의 삭제 히프에서의 삭제는 우선 순위가 가장 높은 값의 삭제를 뜻 하며 이는 곳 루트 노드값의 삭제를 의미합니다.

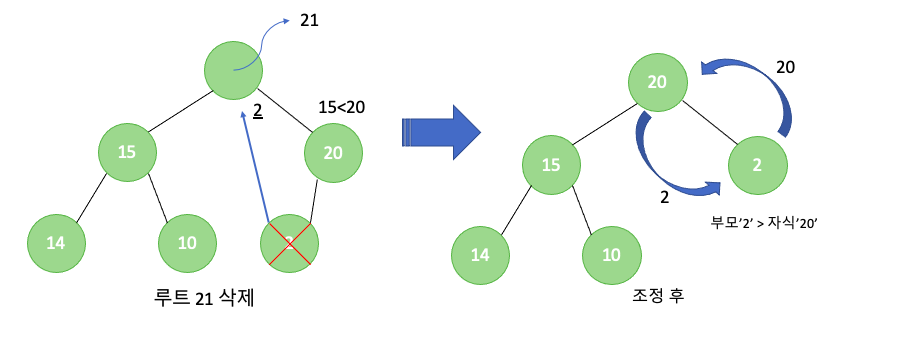
최대 히프의 삭제 과정은 먼저 루트값을 삭제하고 그자리에 맨 아래의 최하위 단일 노드를 삽입합니다.

그 후 루트에 삽입된 값을 루트의 왼쪽, 오른쪽 자식중 더 큰값과 비교한 후 자식의 값이 더 크면 루트의 값과 더큰 자식의 값을 바꿔줍니다.
이러한 조정을 계속 반복하다가 자식이 없거나 자식의 값보다 조정 되는 부모의 값이 커지는 경우 조정을 종료합니다.

[STL] 히프의 멤버함수 및 사용

STL 히프는 주로 vector와 같은 컨테이너를 최대 히프 구조로 만든후 사용됩니다. STL 히프가 최대 히프 형태이기 때문에 일차원 배열이고 루트에는 가장 큰 값이 저장되어 있으며 배열의 index가 증가할수록 값이 커지는 형태를 띄고 있습니다.

• make_heap$($) : 인자로 주어진 범위 만큼 컨테이너의 원소들을 최대 히프 형태로 만든다.
• front$($) : 최대 히프의 루트에 저장된 값을 반환 한다. 즉 제일 큰값을 반환.
• push_heap$($) : 인자로 주어진 범위 만큼 컨테이너의 원소들을 최대 히프 형태로 만듬 $($make_heap후 새로운 원소를 삽입하여 다시 최대 히프 형태로 만들고 싶을때 사용)
• pop_heap$($) : 루트$($최대)값을 반환.
• sort_heap$($) : 최대 히프를 최소 히프 형태로 전환한다.
• is_heap$($) : 최대 히프이면 true 아니면 false 반환.
• is_heap_until$($) : 인자로 주어진 범위 안에서 최대 히프 형태인 원소 까지의 iterator를 반환.

사용 예제

#include<iostream>
#include<vector>
using namespace std;

int main(void)
{
    vector<int> v;
    vector<int>::iterator iter;
    v.push_back(20);
    v.push_back(30);
    v.push_back(50);
    v.push_back(10);
    v.push_back(40);
    //v [20, 30, 50, 10, 40]

    make_heap(v.begin(), v.end()); //벡터 v의 첫 원소부터 끝까지를 히프로 변환
    // v [50, 40, 20, 10, 30] 부모 키값 ≥ 자식 키값
    
    cout<<"히프의 최대 값은 : "<<v.front()<<'\n'; // 50
    v.push_back(60); // 60을 백터 v에 삽입. 히프에는 반영 안됨

    push_heap(v.begin(), v.end()); // 백터 v의 첫 원소부터 끝까지를 히프로 변환. 60 포함
    cout<<"히프의 최대 값은 : "<<v.front()<<'\n'; // 60
    // v [60, 40, 50, 10, 30, 20]

    pop_heap(v.begin(), v.end()); // v [50 40 20 10 30 60]
    v.pop_back(); // v [50 40 20 10 30]
    cout<<"루트값 삭제후 히프의 최대 값은 : "<<v.front()<<'\n'; // 50
    
    sort_heap(v.begin(), v.end()); // v [10 20 30 40 50]
    cout<<"최소 히프로의 변환 : ";
    for(int i=0; i<v.size(); i++) cout<<v[i]<<' ';

    is_heap(v.begin(), v.end()) ? cout<<"'\n최대 히프 맞다.\n" : cout<<"\n최대 히프 아니다(그렇다고 꼭 최소 히프인 것도 아니다)\n";

    return 0;
}

결과

히프의 최대 값은 : 50
히프의 최대 값은 : 60
루트값 삭제후 히프의 최대 값은 : 50
최소 히프로의 변환 : 10 20 30 40 50 
최대 히프 아니다(그렇다고 꼭 최소 히프인 것도 아니다)