[STL] map & 레드블랙트리

STL의 컨테이너 중 하나인 map에 대해서 알아보겠습니다. map은 key와 value로 이루어진 노드의 집합으로 이루어진 트리이며 트리내에 중복된 key값을 갖는 노드는 존재하지 않습니다. 따라서 map은 각각 key와 value에 해당하는 first, second pair 객체로 저장됩니다. STL의 map은 이진탐색트리이며 검색, 삽입, 삭제가 O$($logn)인 레드블랙트리로 구성되어 있습니다.

이진탐색트리$($Binary Search Tree)

레드블랙트리에 대해 설명하기 전에 이진탐색트리에 대해 간략하게 설명 하자면, 이진탐색트리란 특정 key값에 대해 삽입, 삭제, 탐색이 가능한 자료구조를 말합니다. 이진탐색트리의 특징에는 현재 노드의 왼쪽 서브 트리에는 현 노드의 key값보다 작은 key값들이, 오른쪽 서브트리에는 더 큰 key값들이 오게 된다는 것이 있습니다. 이러한 특징은 이진탐색트리의 탐색을 용이하게 하며 중위순회로 이진탐색트리를 순회 할 경우 오름차순으로 정렬된 key값을 얻게됩니다. 아래와 같이 예를 들어보겠습니다.

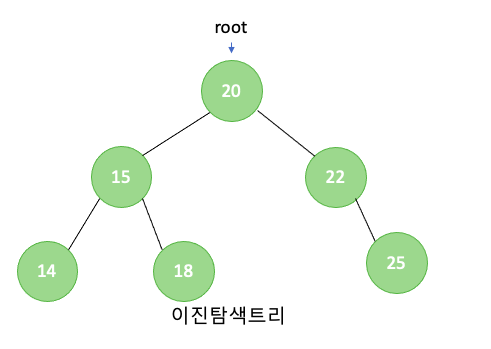
위의 이진탐색트리에서 중위순회는 왼쪽자식->부모->오른쪽자식 노드 순으로 순회하므로 14, 15, 18, 29, 22, 25 과 같이 오름차순으로 정렬됩니다.

탐색 이진탐색트리에서 원하는 key값의 탐색은 찾고자 하는 key값과 root가 가리키는 값을 비교해 가며 이루어 집니다. 만약 찾는 key값과 root가 가리키는 key값이 같다면 root를 반환하고 만약 root의 값이 크다면 왼쪽 서브트리를, root가 작다면 오른쪽 서브트리로 root포인터를 이동하여 위의 과정을 반복하게 됩니다. 만약 리프노드까지 가서도 원하는 key값을 찾지 못하였다면 null을 반환합니다. 탐색에 걸리는 시간은 최악의 경우인 편향트리에 의해 트리의 높이만큼 걸립니다. O(h)

탐색함수의 구현

template<class Type>
BSTNode<Type> *BST<Type>::IterSearch(const Element<Type> &x) //이진 탐색 트리에서 key x의 원소를 탐색
{
    for(BSTNode<Type> *t=root; t;)
    {
        if(x.key == t->data.key) return t; //found
        if(x.key < t->data.key) t=t->LeftChild; //왼쪽 서브트리로 이동
        else t=t->RightChild; //오른쪽 서브트리로 이동
    }
    return 0; //찾는 key값이 트리에 존재하지 않을경우 null 반환
}

삽입 이진탐색트리에서 원소를 삽입할때는 key값에 따라 알맞는 위치에 삽입해야 합니다. 이를 위해 임시 포인터를 뒤따라 가는 포인터가 필요하며 동일한 카값을 가진 원소가 있는 가를 확인한 후, 없으면 뒤따라 가던 포인터가 가리키는 위치에 원소를 삽입합니다. 삽입의 경우에도 시간복잡도는 O(h) 입니다.

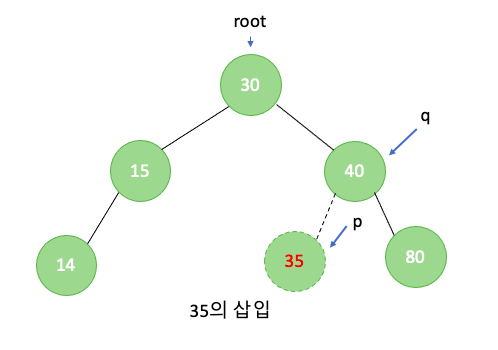
삽입함수의 구현

template<class Type>
Boolean BST<Type>::Insert(const Element<Type> &x)
{//이진 탐색 트리에 x를 삽입
    //x.key를 탐색, q는 p의 부모
    BstNode<Type> *p=root;  //임시포인터 p
    BstNode<Type> *q=0; // p를 뒤따라 가는 포인터 q
    
    while(p)
    {
        q=p;
        if(x.key == p->data.key) return FALSE;// x.key가 이미 존재
        if(x.key < p->data.key) p=p->LeftChild; // p를 왼쪽 자식으로 이동
        else p=p->RightChild; // p를 오른쪽 자식으로 이동
    }
    p=new BstNode<Type>; // p를 재활용하여 삽입을 수행
    p->LeftChild = p->RightChild=0;
    p->data=x;
    if(!root) root = p; // 빈트리일 경우 root가 p를 가리키게 함
    else if(x.key < q->data.key) q->LeftChild = p;
    else q->RightChild = p;
    return TRUE;
}

삭제 이진탐색트리에서 원소의 삭제의 경우 삭제되는 노드의 자식 개수에 따라 삭제 방법이 다릅니다.

1. 리프 노드의 삭제인 경우 $($자식 없음) : 부모의 자식 필드에 0을 삽입합니다.
   

2. 하나의 자식을 갖는 노드의 삭제인 경우 : 삭제된 노드의 자식을 삭제된 노드의 자리에 대체합니다.
   

3. 두개의 자식을 갖는 노드의 삭제인 경우 :

   • 왼쪽 서브트리에서 가장 큰 노드로 대체하거나
   • 오른쪽 서브트리에서 가장 작은 노드로 대체

이때 대체되는 노드의 삭제는 위의 1. 또는 2. 의 경우에 해당합니다.

레드블랙트리$($Red-Black Tree)

위에서 설명한 바와 같이 이진탐색트리의 탐색, 삽입, 삭제 연산의 경우 트리가 편향트리인 경우가 최악의 경우에 해당되며 트리 높이인 O(h)만큼의 시간이 걸리는 것을 알 수 있었습니다. 여기서 알아볼 레드블랙트리 또한 이진탐색트리에 해당되지만 이진탐색트리와 달리 균형 탐색 트리 (balanced search tree) 이기 때문에 편향탐색트리의 모양이 나올수 없는 조건을 갖고 있습니다. 즉, 레드블랙트리에서의 연산은 최악의 경우에도 O(logn)의 시간복잡도를 갖게 됩니다.

레드블랙트리의 조건

다음은 레드블랙트리의 높이를 logn에 바운드 되도록 해주는 조건들입니다.

1. Root Propety - 루트노드의 색깔은 검정이다.
   

2. External Property - 모든 단말노드$($리프)의 색깔은 검정이다
   

3. Internal Property - 빨강 노드의 자식은 검정색 이다. 즉 빨강 노드가 연속으로 나올수 없다.
   

4. Depth Property - 모든 리프노드에서 루트노드까지 가는 경로에서 만나는 블랙노드의 개수는 같다.
   

5. 삽입되는 노드의 색은 빨강이다.

위의 조건에 따라서 값을 삽입하다 보면 아래의 그림과 같이 3. 번 조건에 위배되는 상황이 생기게 됩니다.

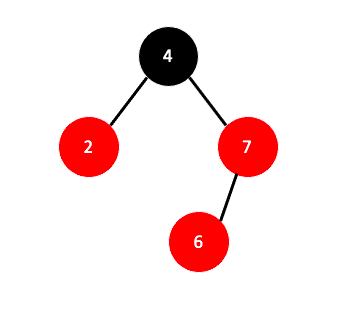
이러한 상황을 Double Red라고 하며 Double Red를 해결하고 위의 조건을 만족시키기 위해 Restructuring 방법과 Recoloring 중 상황에 알맞는 방법을 사용할 수 있습니다.

Restructuring

현재 삽입된 노드$($z)의 부모 형재노드 즉, 삼촌노드$($w)의 색이 검정색인 경우 Restructuring을 수행합니다.

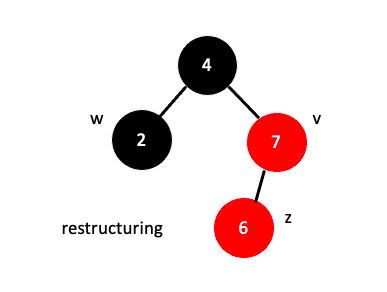
Restructuring은 다음과 같은 순서로 수행됩니다.

1. 삽입되는 값$($z)과 그 값의 부모$($v)와 그 값의 부모의 부모를 오름차순으로 정렬

1. 그 다음 정렬된 값 중 가운데 값을 부모로 만든후 나머지 둘을 자식으로 만듭니다.

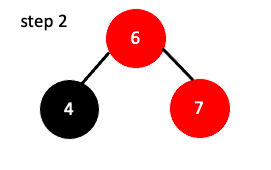
가운데 값 6이 부모가 됐고 부모인 6보다 작은 4가 왼쪽자식, 부모보다 큰 7이 오른쪽 자식으로 배치되었습니다.

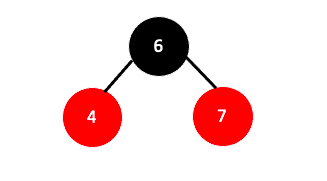
1. 올라간 가운데 값을 검정으로 만들고 나머지 두 자식들을 빨강으로 바꿉니다.

즉 부모와 자식 관계에 맞게 6은 검은색으로 4,7은 빨간색으로 바꿔줍니다.

마지막으로 원래 4의 자식이었던 2를 추가해 주면 restructuring이 끝납니다.

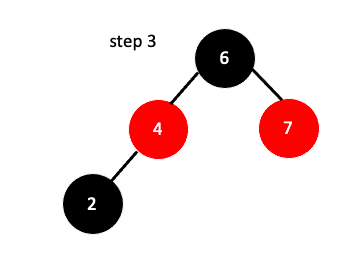
restructuring을 수행한 후 4. 번 조건이 만족하는지 확인해 보면 Double Red를 해결하기 전과 해결 한 후의 Black 노드의 개수에 변화가 없기때문에 다른서브트리에 영향을 끼치지 않게 된다는 것을 알 수 있습니다. 따라서 Double Red를 해결하는데 한번의 restructuring만으로 충분합니다.
restructuring 과정 자체는 상수시간 O$($1)이 걸리지만 원소를 삽입하는데 O$($logn)이 소요되므로 전체 수행시간은 O(logn)이 됩니다.

Recoloring

현재 삽입된 노드$($z)의 부모 형재노드 즉, 삼촌노드$($w)의 색이 빨강색인 경우 Recoloring을 수행합니다.

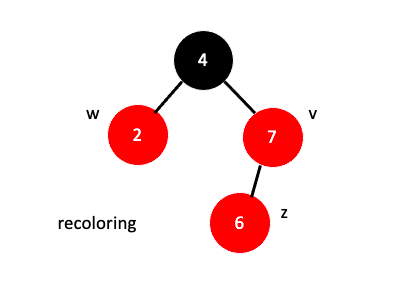
Recoloring은 다음과 같은 순서로 수행됩니다.

1. 삽입된 노드$($z)의 부모와 그 형제를 검정으로 바꾸고 부모의 부모를 빨강으로 한다.

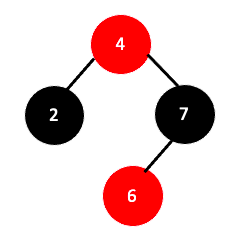
이때 4가 루트노드인 경우 1. 번 조건에 의해서 다음과 같이 검정색이 됩니다.

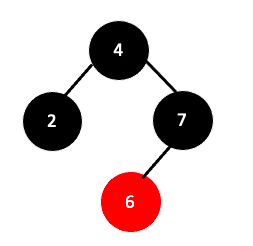
하지만 만약 4가 루트노드가 아닌 위의 트리가 어떤 임의의 레드블랙트리의 서브트리라고 생각해 본다면 4는 빨강색이 4위에 아래와 같이 또 빨강노드가 오게 된다면 다시 Double Red 상황이 발생하고 4의 부모의 형제노드 색깔에 따라 Recoloring과 Restructuring중 하나를 또 수행해야 하는 경우가 생길 수 있습니다.

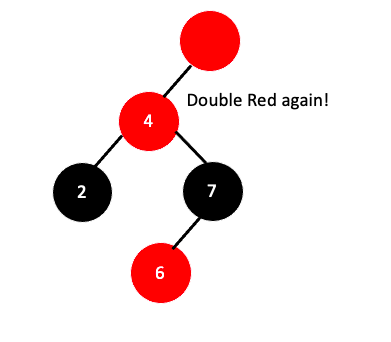
이때 Restructuring을 수행할 경우 Restructuring은 다른 서브트리에 영향을 끼치지 않으므로 Double Red는 더이상 발생하지 않고 balancing을 종료할 수 있습니다. 하지만 Recoloring의 경우 최악에 root까지 Recoloring을 반복할 수 있습니다.
Recoloring도 마찬가지로 수행에 상수시간 O$($1)이 걸리며 값을 삽입하면서 삽입할 위치를 찾는데 O$($logn)이 소요되므로 root까지 recoloring을 하는 최악의 경우에도 O(logn)시간이 소요됩니다.
Recoloring과 Restructuring을 거쳐 레드블랙트리를 완성했을때 4. 번 조건인 “Black Depth”에 따라 어느 리프노드에서 루트노드까지 가더라도 거치는 검정노드의 수는 같아야 합니다. 이때 물리적으로 가장 짧은 Black Depth의 경우 리프노드에서 루트노드까지 검정노드만 거치는 경우이며 가장 긴 Black Depth의 경우 “검정-빨강-검정-빨강…검정” 과 같이 Double Red를 피하는 형태가 가장 깁니다. 이때 가장 길고 짧은 Black Depth는 최대 2배밖에 차이나지 않습니다. 이와 같이 balance하기 때문에 레드블랙트리의 높이가 O(logn)에 바운드 될 수 있는 것입니다.

[STL] map의 멤버함수 및 사용법

#include<map>

map<key자료타입, value자료타입, 비교함수> m; 비교함수 default = 오름차순

• begin$($) : 첫번째 원소의 랜덤 접근 반복자를 반환
• end$($) : 마지막 원소 다음의$($미사용 영역) 반복자를 반환
• clear$($) : 컨테이너안의 저장된 모든 원소를 삭제
• empty$($) : 컨테이너가 비었으면 true, 아니면 false를 반환
• erase$($) : 특정 위치의 원소 또는 지정 범위의 원소들을 삭제
• insert$($) : 첫번째 인자인 iterator가 가리키는 위치에 두번째 인자 값 삽입. 삽입 위치의 뒤에 있던 원소들의 인덱스는 한칸씩 뒤로 밀림.
• size$($) : 원자의 개수를 반환
• find$($) : key와 관련된 원소의 반복자를 반환
• rbegin$($) : 역박향으로 첫번째 원소의 반복자를 반환
• rend$($) : 역방향으로 마지막 원소 다음의 반복자를 반환
• upper_bound$($) : 지정한 key 요소를 가지고 있다면 해당 위치 다음 위치의 반복자를 반환
• lower_bound$($) : 지정한 key 요소를 가지고 있다면 해당 위치의 반복자를 반환
• operator[] : 지정한 키값으로 원소 추가 및 접근. ex$)$ m[1];

참조

https://zeddios.tistory.com/237