2차원 배열 누적합 알고리즘 [파이썬 코드]

2차원 배열의 부분합을 구하기 위해서는 보통 중첩 for문을 사용하여 구할수 있다.

하지만 이는 시간복잡도 O(N^2) 시간이 소요되기 때문에 그다지 효율적인 방법이라고 볼수는 없다.

누적합 알고리즘을 통해서 더 빠른 시간안에 부분합을 구하는 방법을 알아보도록 하겠다.

누적합

먼저 1차원 배열을 예로 누적합에 대해서 알아보도록 하자.

arr = [2, 5, 6, 7, 9]

다음과 같은 1차원 배열에서 arr[1] 부터 arr[3] 까지의 합을 구하기 위해서는 3개의 원소값을 반복문을 돌면서 참조해야한다. O(N)

만약 0번째 인덱스부터 해당 인덱스 까지의 누적합을 저장하는 별도의 배열을 선언해 주면 반복문 없이 특정 범위내의 누적합을 구할 수 있다.

sum_arr = [2, 7, 13, 20, 29]

• sum_arr[i]는 arr[0] ~ arr[i]까지의 모든 원소의 합을 값으로 갖는다.

• arr[i] ~ arr[j] 까지의 부분합 = sum_arr[j] - sum_arr[i - 1]

2차원 누적합

1차원 배열의 누적합 배열이 1차원 배열이였듯, 2차원 배열의 누적합 또한 2차원 배열이다.

누적합 배열을 통해서 2차원 배열의 특정 구간의 원소합을 O(1) 시간안에 구할 수 있다.

2차원 누적합 배열 구하기

1. a(i, j)에서 행방향으로 누적합 구하기
2. 행 누적합에 대해서 열방향으로 누적합 구하기

출처 - ohdowon064.log

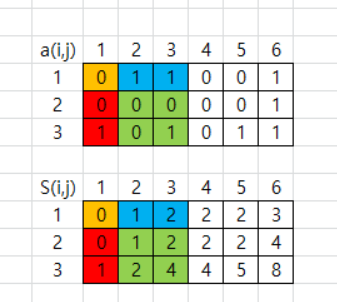
S(i, j)는 a(1, 1)과 a(i, j)를 양 대각 끝 꼭짓점으로 하는 직사각형 범위 면적 안의 모든 a원소의 합으로 정의된다.

초록색으로 표시된 a(2, 2) ~ a(3, 3)의 부분합을 구하기 위해서는 다음 과정을 거친다.

출처 - ohdowon064.log

1. S(3, 3)에서 S(3, 1) S(1, 3)을 뺀다.

2. S(1, 1)은 S(3, 1), S(1, 3)에 의해서 두번 뺄셈이 되었기 때문에 S(1, 1)을 더해준다.

a[r1][c1] 부터 a[r2][c2] 까지의 부분 배열의 합을 Range(r1, c1, r2, c2)라고 하면 다음과 같은 수식을 세울수 있다.

Range(r1, c1, r2, c2) = S(r2, c2) - S(r1, c2) - S(r2, c1) + S(r1, c1)

파이썬 코드

# 부분합 구하기
def accum(S, r1, c1, r2, c2):
    return S[r2][c2] - (S[r1][c2] + S[r2][c1]) + S[r1][c1]


# 누적합 배열 구하기
def get_sum_arr(arr):
    # 행의 합 구하기
    sum_arr = [[sum(arr[i][ : j + 1]) for j in range(len(arr[0]))] for i in range(len(arr))]

    # 열의 합 구하기
    for i in range(len(sum_arr) - 1):
        for j in range(len(sum_arr[0])):
            sum_arr[i + 1][j] += sum_arr[i][j]
        
    return sum_arr


arr = [[0, 1, 1, 0, 0, 1],
       [0, 0, 0, 0, 0, 1],
       [1, 0, 1, 0, 1, 1]]

sum_arr = get_sum_arr(arr)

print(accum(sum_arr, 0, 1, 2, 4))

참고 자료

• https://velog.io/@ohdowon064/Algorithm-2%EC%B0%A8%EC%9B%90-%EB%B0%B0%EC%97%B4-%EB%B6%80%EB%B6%84%ED%95%A9-%EB%88%84%EC%A0%81%ED%95%A9-%EA%B5%AC%ED%95%98%EA%B8%B0