[Algorithm] 재귀함수 tracing

재귀 함수의 수행 과정

재귀 함수란 자기 자신을 반복해서 호출하는 함수를 말합니다. 대부분의 재귀함수는 반복문으로 표현가능하며 반복문 또한 재귀함수로 표현이 가능합니다. 재귀함수는 연속된 함수호출을 종료하기 위한 base case와 recursive case로 구성됩니다.

재귀함수 호출시 함수호출문 아래의 문장은 잠시 수행을 멈추고 재귀함수가 base case를 만나 반환되며 다시 자신을 호출했던 함수로 복귀하면서 나머지 함수호출문 아래의 문장이 수행됩니다.

아래의 예제를 통해 재귀함수의 수행과정에 대해 알아보겠습니다.

void fun1(int n)
{
    if(n>0)
    {
        printf("%d ",n);
        fun1(n-1);
    }
}

int main(void)
{
    int x=3;
    fun1(x);
}

위의 프로그램을 실행하면 초기의 fun1$($3)은 3을 출력하고 fun1$($2)를 호출합니다. fun1$($2)는 2를 출력하고 fun1$($1)을 호출합니다. fun1$($1)도 1을 출력하고 fun$($0)을 호출하지만 if(n>0)의 조건문에 의해 아무것도 수행하지 못하고 return하여
fun$($0) ->fun$($1) -> fun$($2) -> fun$($3) 순으로 반환됩니다. 이와 같은 과정을 tracing tree로 나타내면 다음과 같습니다.

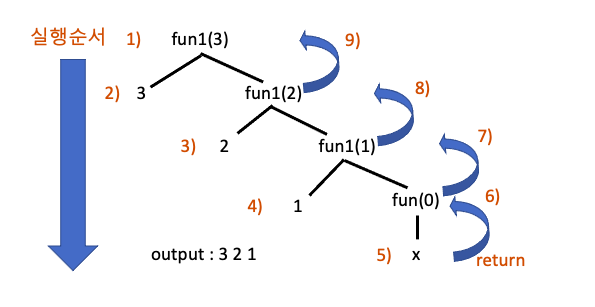
1$)$ ~ 5$)$의 함수호출 단계를 calling phase이라 하며 6$)$ ~ 9$)$ 함수반환 단계를 returning phase라고 합니다. 즉 재귀함수는 calling, returning 두 단계로 이루어져 있습니다.

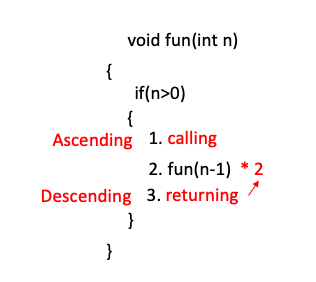
또한 함수호출문 이후에 나오는 연산이나 함수도 returning phase에서 수행됩니다.

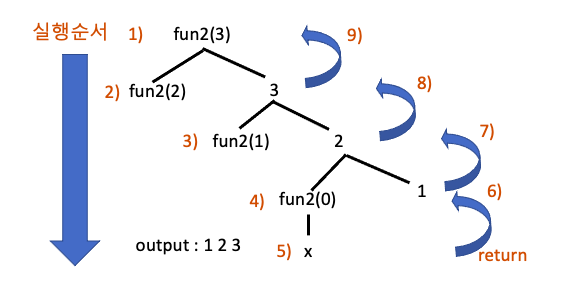
위의 프로그램의 출력결과가 3 2 1이 었다면 다음 프로그램의 출력결과는 어떻게 될까요?

void fun2(int n)
{
    if(n>0)
    {
        fun2(n-1);
        printf("%d ",n);
    }
}

int main(void)
{
    int x=3;
    fun2(x);
}

fun2는 fun1과 다르게 함수호출문 이후에 출력문이 존재합니다. 재귀함수에서 함수호출문 아래의 문장은 returning phase에서 수행되므로 출력 결과는 1 2 3 이 되며 tracing tree는 다음과 같습니다.

재귀 함수에서의 스택

함수가 호출되면 함수의 매개변수, 지역변수, return address 등의 데이터가 메모리 상의 스택에 저장됩니다. fun2 함수를 재귀호출 했을 경우 스택에 저장되는 과정을 살펴보겠습니다.

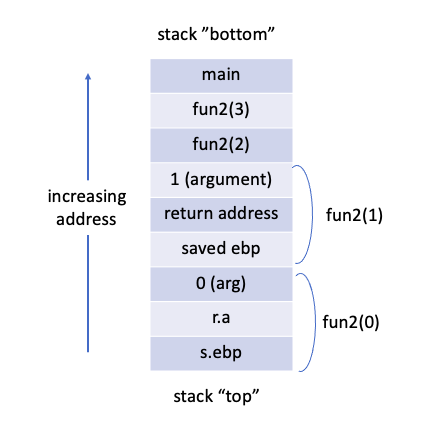
calling phase, 즉 1) ~ 5), fun2(0)까지 호출되었을때 스택에는 다음과 같이 함수들이 쌓여있습니다. 이때 주의할 점은 스택이 실제로 메모리 상에서는 위에서 아래로 자라는 형태로 되어있으며 값의 삽입과 삭제는 top에서 이루어 진다는 점입니다. fun2(0)의 return이 수행되면 스택에서 fun2(0)은 삭제되고 그 다음 fun2(1)이 삭제되고를 반복하게 됩니다.

재귀함수의 다양한 타입들

재귀함수는 함수호출문의 위치에 따라 다양한 종류로 나뉘게 됩니다.

1. Tail Recursion 위의 fun1함수와 같이 함수호출문 후에 수행할 문장이 없는, 즉 returning phase가 없는 재귀함수의 경우를 Tail Recursion이라 합니다.
   

2. Head Recursion fun2함수와 같이 함수호출문 이전에 수행할 문장이 없는, 즉 calling phase가 없는 재귀함수의 경우를 Head Recursion이라 합니다.
   

3. Tree Recursion 한 함수문에서 자기 자신을 한번 이상 호출하는 경우, 이러한 재귀함수를 Tree Recursion이라 합니다.

void fun(int n)
{
    if(n>0)
    {
        printf("%d ", n);
        fun(n-1);
        fun(n-1); //자기 자신을 한번 이상 호출
    }
}

int main(void)
{
    fun(3);
}

위의 프로그램에서 먼저 오는 fun함수가 fun$($0)까지 수행을 마친후 자신을 호출했던 fun$($1)으로 돌아가면서 returning phase를 수행하고 두번째 fun함수에 1이 인자로 전달되면서 수행됩니다. 이를 반복하는 tracing tree는 아래와 같습니다.

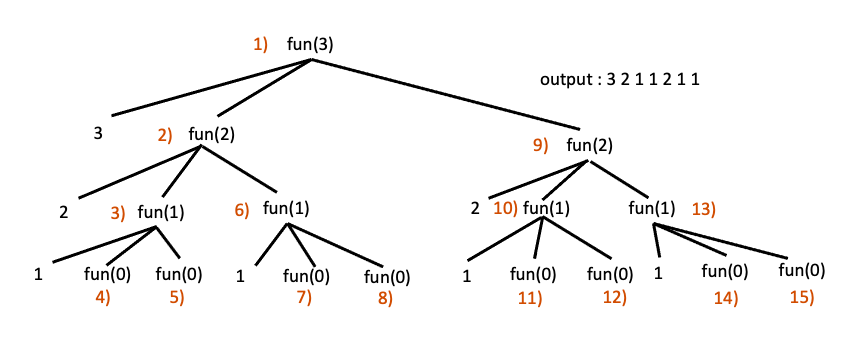
위의 트리의 각 level에서의 함수 수행 횟수를 세어 보면 level 1에서 1번, level 2에서 두번, level 3에서 4번, level 4에서 8번 인것을 알 수 있습니다. 즉, 함수가 총 1+2+4+8=15번 수행되었고 이는 곧 2⁰ + 2¹ + 2² + 2³ = 2³⁺¹ - 1 과 같습니다.

따라서 만약 함수가 fun$($n) 일 경우 총 2ⁿ⁺¹ - 1 번 함수가 수행되는 것을 알 수 있고 이는 시간복잡도 O$($2ⁿ) 을 나타내게 됩니다.

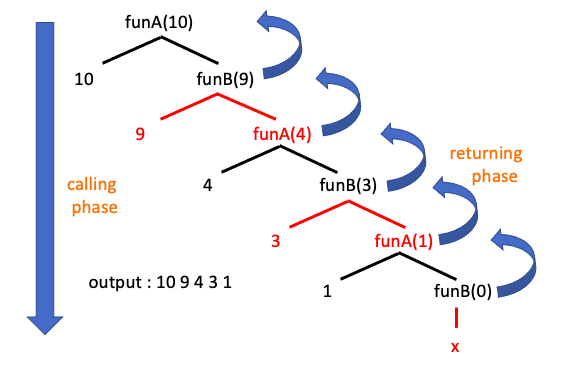
1. Indirect Recursion 두 개 이상의 함수들이 서로간에 호출하면서 사이클을 이룰 경우 이러한 재귀함수를 Indirect Recursion이라 합니다.

void funA(int n)
{
    if(n>0)
    {
        printf("%d", n);
        funB(n-1);
    }
}

void funB(int n)
{
    if(n>1)
    {
        printf("%d", n);
        funA(n/2);
    }
}

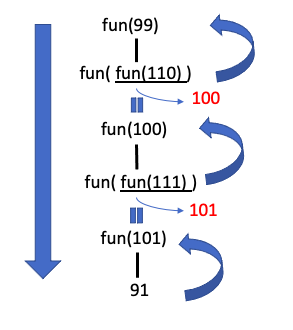
1. Nested Recursion 재귀 함수가 자기 자신을 호출할때 매개변수로 자신을 전달하는 경우를 Nested Recursion이라 합니다.

int fun(int n)
{
    if(n>100)
        return n-10;
    else
        return fun(fun(n+11));
}

int main(void)
{
    fun(99);
}

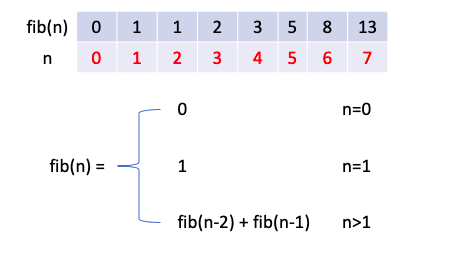
예제_피보나치 함수

재귀 함수로 구현할 수 있는 대표적인 문제중에는 피보나치 수가 있습니다. 피보나치 수는 0과 1로 시작하며 바로 앞의 두 수의 합이 다음 피보나치 수가 됩니다. 0, 1, 1, 2, 3, 5, 8, 13 … 이를 base case와 recursive case로 나누면 아래와 같이 됩니다.

이를 재귀 함수로 구현해보면 다음과 같습니다.

int fibo(int n)
{
    if(n<=1)
        return n;
    else
        return fibo(n-2)+fibo(n-1);
}

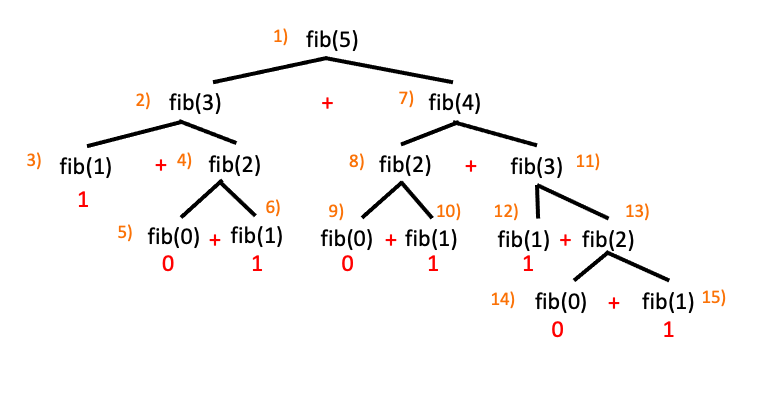
하지만 위의 프로그램의 경우 fibo(n-2)+fibo(n-1); 문에 의해 시간복잡도 O$($2ⁿ)가 걸리게 되는데 이는 상당히 비효율 적입니다.

프로그램의 성능 개선을 위해 위의 트리에서 주목해야 할 점은 한번 수행되어 값을 이미 구한 함수를 반복해서 수행하고 있다는 점입니다. 예를 들어 수행 순서 5$)$ 에서 fib$($0)의 값을 구했다면 값을 저장해 놓고 후에 수행되는 9$)$, 14$)$에서 fib$($0)을 또 호출할 필요없이 미리 저장해 놓은 값을 사용할 수 있습니다. 이러한 접근방법을 메모이제이션 (memoization)이라 부릅니다.

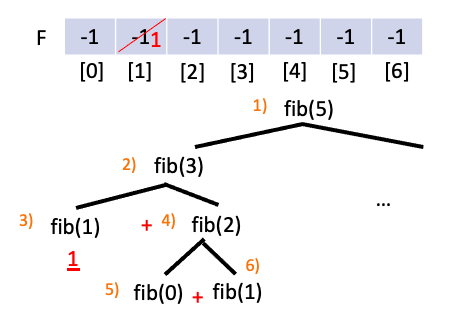
메모이제이션을 통한 피보나치 구현 한번 구한 함수값은 배열에 저장된 후 재사용 됩니다. 통상 초기의 배열 원소값들은 전부 값이 구해지지 않았다는 것을 뜻하는 -1로 초기화 시켜줍니다. 그 다음 상위 값을 구하기 위해 필요한 fib$($0)과 fib$($1)중 먼저 만나는 값은 3$)$에서 만나는 fib$($1)이고 배열 F[1]==-1 이므로 fib$($1)을 수행한 후 값을 F[1]에 저장해 줍니다.

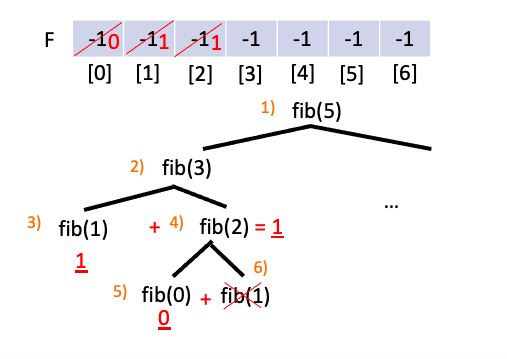
그 다음 5$)$에서 fib$($0)의 값을 구하여 F[0]에 저장해 주고 6$)$의 fib$($1)을 호출할 필요없이 이미 F[1]에 저장된 값과 F[0]에 저장된 값을 이용하여 fib$($2)를 구한 후 F[2]에 저장해 줍니다.

이와 같은 과정을 반복하면 총 6번만의 함수 호출로 fib$($5)의 값을 구할 수 있습니다.

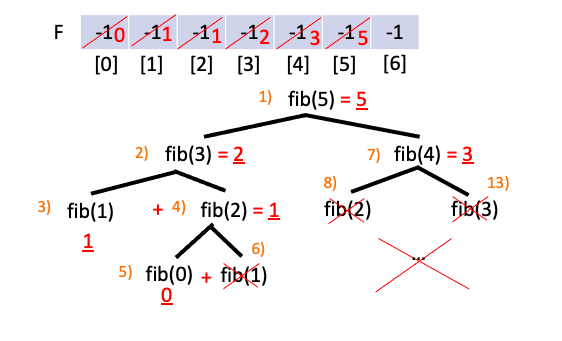
따라서 fib$($n)은 총 n+1 번의 함수호출을 하는 것을 알 수 있으며 이는 시간복잡도로 O$($n), 선형 시간이 걸리게 됩니다. 메모이제이션을 통해 수행 시간을 O$($2ⁿ) 에서 O$($n) 까지 개선 시킨것을 알 수 있습니다.

int mfib(int n)
{
    if(n<=1)
    {
        F[n]=n;
        return n;
    }
    else
    {
        if(F[n-2]==-1)
            F[n-2] = mfib(n-2);
        if(F[n-1]==-1)
            F[n-1] = mfib(n-1);

        F[n]=F[n-2]+F[n-1];
        return F[n-2] + F[n-1];
    }
}

int main(void)
{
    for(int i=0; i<7; i++) 
        F[i]=-1;

    printf("%d \n", mfib(5));
    return 0;
}

재귀 함수는 수학적 공식을 구현하는데 편리하다는 장점이 있지만 함수를 반복적으로 호출하고 반환하면서 스택이 새로 만들어지고 삭제되는 과정을 반복하기 때문에 반복문에 비해 수행 시간이 오래 걸린다는 단점이 있다는 것을 유의해야 합니다. 다음은 피보나치 함수를 반복문을 사용하여 구현한 것입니다.

int fibo(int n)
{
    int t0=0, t1=1;
    int sum=0;

    if(n<=1) return n;

    for(int i=2; i<=n; i++)
    {
        sum=t0+t1;
        t0=t1;
        t1=sum;
    }
    return sum;
}

int main(void)
{
    printf("%d\n", fibo(10));
}