[Algorithm] 고속 거듭제곱 알고리즘

거듭제곱을 그냥 구하는것은 어렵지 않다.

가령 2의 거듭제곱인 2^k에서 k = 10이라고 한다면 2를 10번 곱해주면 된다.

int ans = 1;

for(int k=0; k<10; k++)
    ans *= 2;

이런식으로 2¹⁰을 구할 수 있다.

하지만 지수 k의 값이 커지면 위의 알고리즘의 시간복잡도는 O$($N)이므로 시간초과에 걸리게 된다.

고속 거듭제곱 알고리즘

고속 거듭제곱의 핵심 아이디어는 분할정복이다.

구해야 하는 거듭제곱을 큰값에서 부터 작게 쪼개어 나가다 보면 답을 구할 수 있다.

밑이 a, 지수가 k라고 가정해보자.

a^k를 구하고자 할때 지수 k값이 홀수 이냐 짝수 이냐에 따라 다음과 같이 나뉘게 된다.

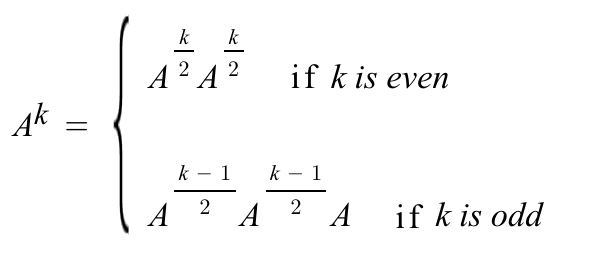
위의 식으로 자수 k가 1이 될 때까지 반복해주면 거듭제곱을 빠르게 구할수 있다.

#define ll as long long

ll fast_pow(ll a, ll k)
{
    // a는 밑, k는 지수
    ll ans = 1;
    while(k)
    {
        // 지수가 홀수인 경우에만 ans에 밑을 한번 더 곱한다.
        if(k % 2) ans *= a;

        a *= a; // 홀수, 짝수 상관없이 밑을 제곱
        k /= 2; 
    }
    return ans;
}

2³³을 지수를 반으로 나누는 방식인 고속 제곱 알고리즘으로 구하면 가존의 33번 연산에서 5번 연산 만으로 답을 구할 수 있다.

지수를 2로 계속 나눠주기 때문에 결과적으로 log₂N 번 돌아간다. 결국 **O$($logN) 시간복잡도를 갖게된다.