[Algorithm] KMP 문자열 검색 알고리즘

KMP 알고리즘 이란?

KMP 알고리즘은 알고리즘을 고안한 세명의 이름 $($Knuth, Morris, Pratt)의 앞 글자를 따와 KMP 알고리즘이라 불리게 되었습니다.

KMP 알고리즘은 텍스트에서 부분 문자열을 검색하는데 있어 유용한 알고리즘 입니다. 예를 들어 “ABCABABCDE” 문자열에서 부분 문자열 “ABC”가 총 몇번 등장하는지 알아봅시다. 단순하게 부분 문자열 “ABC”의 개수를 새는 방법은 다음과 같이 “ABC” 부분 문자열을 한칸씩 옮겨 가며 같은지 비교하는 방법입니다.

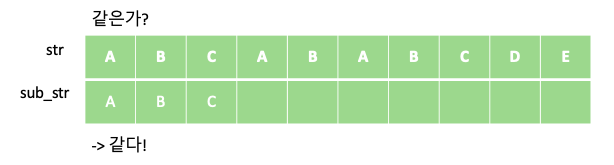
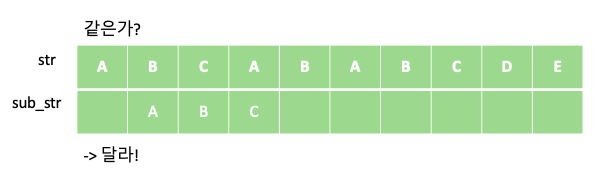
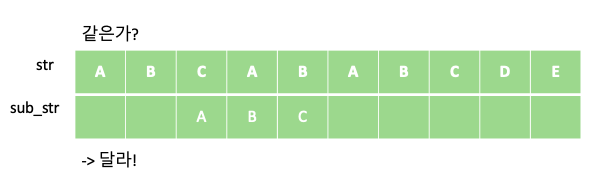
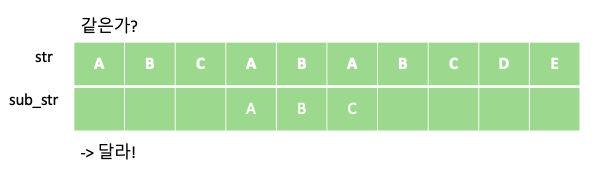
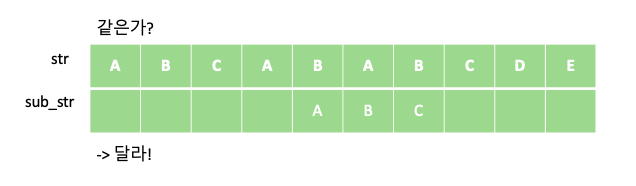
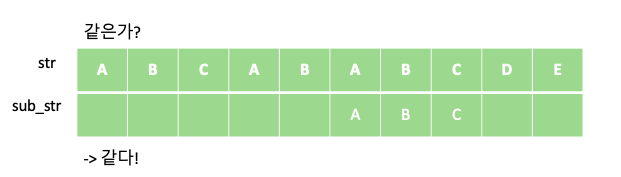
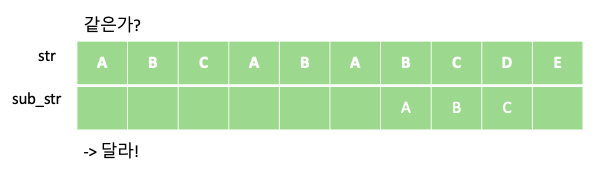
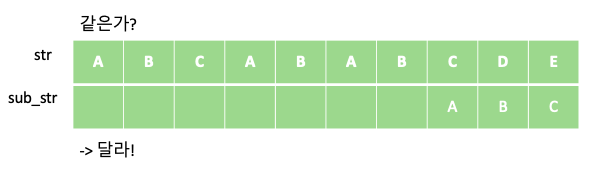
위의 과정을 통해서 주어진 문자열 “ABCABABCDE” 안에 부분 문자열 “ABC”가 총 두번 등장 하는 것을 알 수 있습니다. 해당 과정의 시간 복잡도는 문자열의 길이를 N, 부분 문자열의 길이를 M이라 할때 각 문자열의 인덱스에 대해 부분 문자열이 일치하는지 일일이 비교하므로 O$($NM)이 걸리게 됩니다.

하지만 KMP 알고리즘을 이용한다면 시간 복잡도를 O$($N+M)까지 단축시키는게 가능합니다.

KMP 알고리즘 이해를 위한 사전 개념

KMP 알고리즘을 이해하고 활용하기 위해서는 두가지 개념을 이해할 필요가 있습니다.

1. 접두사$($prefix), 접미사$($suffix)

“apple”의 접두사와 접미사를 예를 들면 접두사와 접미사에 대해 이해될 것 입니다.

**** a
ap
app
appl
apple

**** e
le
ple
pple
apple

1. pi$($table) 배열

pi[i]는 주어진 문자열의 0~i 까지의 부분 문자열 중에서 접두사와 접미사가 일치하는 최대 길이 입니다. (이때 prefix가 0~i 까지의 부분 문자열과 같으면 안된다.)

이해를 돕기위해 예시를 들어 보겠습니다.

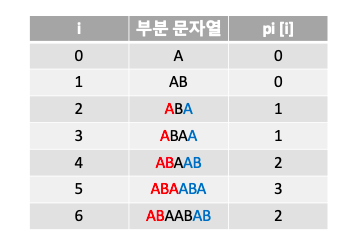
접두사와 접미사가 일치하는 최대 길이 $($table[i]) 구하기

그렇다면 문자열의 접두사와 접미사의 최대 길이인 p[i]값은 어떻게 구할 수 있을까요? 문자열의 인덱스를 나타내는 변수 i와 j를 사용하여 아래와 같은 순서의 과정을 통해서 최대 일치 길이값을 구하는 함수를 구현할 수 있습니다.

1. 모든 문자를 하나씩 검사를 하면서 j가 0보다 크고 인덱스 i번째 문자와 j번째 문자가 같지 않으면 j에서 1을 뺀 위치의 인덱스 값 위치로 이동한다 $($i만 증가, j는 1 감소).

2. i번째 인덱스의 값과 j번째 인덱스의 값이 일치하는 경우 i번째 인덱스의 값은 j위치 $($index)에 1을 더한값이 되며 j의 위치를 1증가 시켜준다 $($i, j 둘다 증가).

부분 문자열 “ABAABAB”을 예로 들어서 최대 일치길이를 구하는 과정을 알아보겠습니다.

초기 상태는 위와 같습니다. j=A 이고 i=B이기 때문에 i≠j 이므로 i의 인덱스에 j의 인덱스 값 0 을 넣고 i를 1 증가 시킵니다. ->

j=A 이고 i=A, i=j 이기 때문에 i의 인덱스에 j의 위치$($index) 값 0에 1을 더한 값인 1을 넣고 i와 j를 1 증가 시킵니다. ->

j=B 이고 i=A이기 때문에 i≠j 이므로 j를 1 감소 시킨 위치$($A)의 인덱스 값인 0, 즉 index[0]$($A) 으로 j를 이동 시킵니다. ->

이제 j와 i의 값이 A로 일치 하므로 i의 인덱스에 j의 위치$($index) 0에 1을 더한 값인 1을 넣고 i와 j를 1 증가 시킵니다. ->

j와 i는 B로 일치하기 때문에 i의 인덱스에 j의 위치$($index) 1에 1을 더한 값인 2를 넣고 i와 j를 1 증가 시킵니다. ->

i와 j의 값이 A로 일치 하기 때문에 i의 인덱스에 j의 위치 2에 1을 더한 값인 3을 넣고 i와 j를 1 증가 시킵니다. ->

j=B, i=A, 즉 i≠j 이므로 j를 1 감소 시킨 위치의 인덱스 값인 1, 즉 index[1]$($B) 로 j를 이동 시킵니다. ->

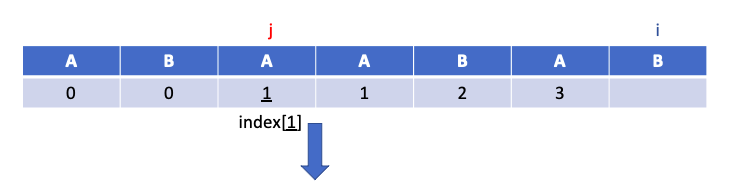
j=i=B 로 일치하므로 i의 인덱스에 j의 위치 1에 1을 더한 값인 2를 넣습니다. 부분 문자열의 끝 까지 pi 테이블이 완성 되었으므로 과정을 종료합니다. ->

위의 과정을 통해 구한 pi 테이블의 각 숫자 들은 해당 인덱스 위치 까지의 최대 일치 길이를 의미 합니다.

위의 테이블을 통해 “ABAABAB” 문자열의 접두사와 접미사의 일치하는 부분은 “AB”이며 최대 일치 길이는 2라는 것을 알 수 있습니다.

이번에도 마찬 가지로 “ABAABA” 문자열의 접두사와 접미사의 일치 부분은 “ABA이며 최대 일치 길이는 3이라는 것을 알 수 있습니다. 다음의 결과 또한 마찬 가지 입니다.

이러한 최대 일치 길이 테이블을 구하는 과정을 소스코드로 구현해 보겠습니다.

#include<iostream>
#include<vector>
#include<string>
using namespace std;

vector<int> makeTable(string pattern)
{
    int patternSize = pattern.size();
    vector<int> table(patternSize, 0);
    int j = 0;
    for(int i=1; i<patternSize; i++)
    {
        while(j>0 && pattern[i] != pattern[j]) // i와 j가 일치하지 않는 경우
            j = table[j-1]; // j를 j에서 1을 뺀 인덱스 값 위치로 이동
        
        if(pattern[i]==pattern[j]) // i와 j가 일치하는 경우
            table[i] = ++j; //i의 인덱스에 j의 위치에 1을 더한 값을 넣고 j 증가(i는 for문에 의해서 증가됨)
    }
    return table; // 최대 일치 길이를 표현하는 table을 반환
}

int main(void)
{
    string pattern = "ABAABAB"
    vector<int> table = makeTable(pattern);
    for(int i=0; i<table.size(); i++) cout<<table[i]<<' ';
    return 0;
}

O/P : 0 0 1 1 2 3 2

KMP 알고리즘 원리 및 활용

KMP 알고리즘의 원리는 앞에서 배운 접두사와 접미사의 공통된 부분을 활용하여 불필요한 중간 과정을 점프하는 것 입니다.

문자열 “ABCDABCDABEE” 에서 부분 문자열 “ABCDABE”를 찾는다면 index 0~5 까지는 문자열이 일치하고 index 6에서 다르다는 정보를 활용하여 두 번째 테이블과 같이 중간 과정을 점프 할 수 있습니다.

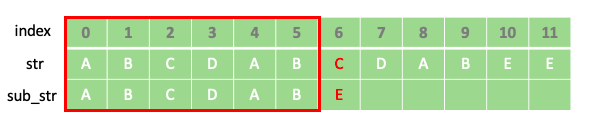
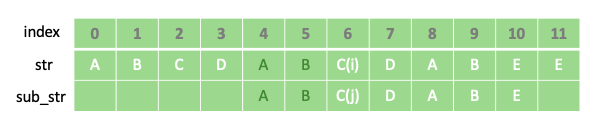
위와 같은 점프가 가능했던 이유는 일치하는 부분이였던 “ABCDAB”에서 파란색 박스로 표시된 접두사와 접미사인 “AB”가 일치 했기 때문입니다. 즉 “ABCDAB”의 최대 일치 길이는 pi[5]=2 인 것 입니다.

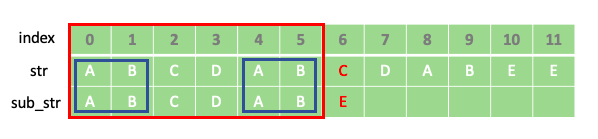
또 다른 예를 들어 보겠습니다. 다음과 같은 문자열 str과 부분 문자열 sub_str이 있다면 서로 다른 문자가 발견 될때 까지 문자들을 하나씩 비교합니다.

위와 같이 일치하지 않는 경우가 발생했을때 앞에서 구현했던 최대일치길이 테이블을 이용하여 부분 문자열의 접두사와 일치하는 str의 접미사 부분으로 점프하여 비교를 진행 합니다.

비교를 진행하다가 또 다시 일치하지 않는 경우가 발생하며 이때도 부분 문자열의 접두사와 일치하는 str의 접미사 부분으로 점프하여 비교를 진행 합니다.

마침내 부분 문자열과 일치하는 문자열을 발견 하였습니다. 하지만 아직 문자열 전체를 전부 확인 하지 않았으므로 다시 부분 문자열의 접두사와 일치하는 str의 접미사 부분으로 점프하여 비교를 진행 합니다.

따라서 총 두번 부분 문자열과 매칭 된다는 것을 알 수 있습니다. 또한 위의 과정을 통해서 긴 문자열의 길이 만큼만 비교를 하면 되기 때문에 KMP 알고리즘의 시간 복잡도는 O(N)이 되는 것 입니다.

#include<iostream>
#include<vector>
#include<string>
using namespace std;

void KMP(string parent, string pattern)
{
    vector<int> table = makeTable(pattern);
    int patternSize = pattern.size();
    int parentSize = parent.size();
    int j = 0;

    for(int i=0; i<parentSize; i++)
    {
        while(j>0 && parent[i] != pattern[j]) // 일치 하지 않으면
            j = table[j-1]; //j를 이전단계 위치로 이동 

        if(parent[i] == pattern[j])
        {
            if(j == patternSize - 1)
            {
                cout << i - patternSize + 2 << 번째 에서 찾았습니다! <<'\n';
                j = table[j]; // 점프를 위한 j값 갱신 
            }
            else
                j++;
        }
    }       
}

int main(void)
{
    string parent = "ABCDABCCDABEE";
    string pattern = "ABCDABE";
    KMP(parent, pattern);
    return 0;
}

풀어보면 좋은 문제

• 찾기 $($BOJ_1786)