[Alogorithm] 깊이 우선 탐색 DFS

그래프 표현 방식

• 인접 행렬 : 2차원 배열로 그래프의 연결 관계를 표현

• 인접 리스트 : 리스트로 그래프의 연결 관계를 표현

깊이 우선 탐색 (DFS)이란 그래프 상의 모든 정점을 방문할 때 보다 깊은 것을 먼저 탐색하는 알고리즘입니다.

깊이 우선 탐색에서는 스택을 사용하여 되돌아갈 정점을 저장하지만 컴퓨터에서는 구조적으로 항상 스택의 원리를 사용하기 때문에 굳이 스택을 사용하지 않더라도 구현 가능합니다.

깊이 우선 탐색의 단계

1. 출발 정점 v를 방문하고 v를 스택에 삽입합니다.
   
2. 스택의 최상단 노드를 확인합니다.
   
3. 최상단 노드에게 방문하지 않은 인접 노드가 있으면 스택에 넣고 방문 처리합니다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 뺍니다.
   
4. 방문이 안된 정점으로 더 이상 갈 수 없을 때, 즉 스택이 빌때까지 2,3 단계를 반복합니다.

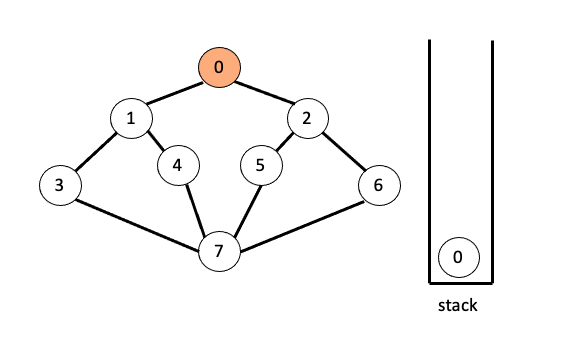
최상단 노드인 0을 방문 처리해 주고 스택에 삽입하였습니다. 그 다음 스택의 최상단 노드인 0과 인접한 노드 중에서 방문하지 않은 노드를 임의로 골라 스택에 삽입하고 방문 처리해 줍니다. 1과 2중 1을 방문해 주겠습니다.

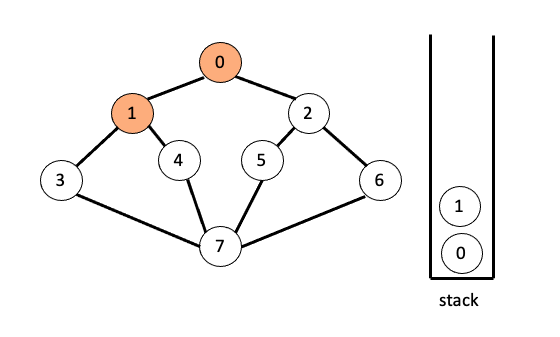
그 다음 1과 인접한 노드 3을 방문한 후 스택에 넣고

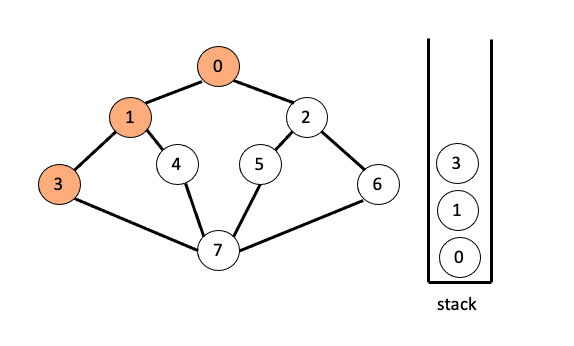
3과 인접한 노드 7을 방문하고 스택에 넣고,

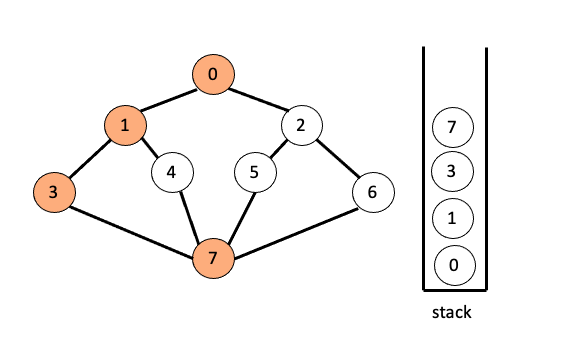
7과 인접한 노드 4를 방문하고 스택에 넣으면 다음과 같이 됩니다.

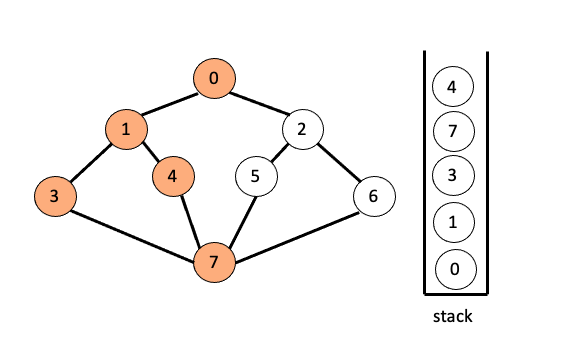
이때 4에 인접한 노드 중 방문 하지 않은 노드가 없으므로 스택의 최상단 노드인 4를 pop해 줍니다.

그럼 스택의 최상단 노드는 7이 되고 7의 인접 노드중 방문 하지 않은 노드인 5를 방문하고 스택에 넣어줍니다.

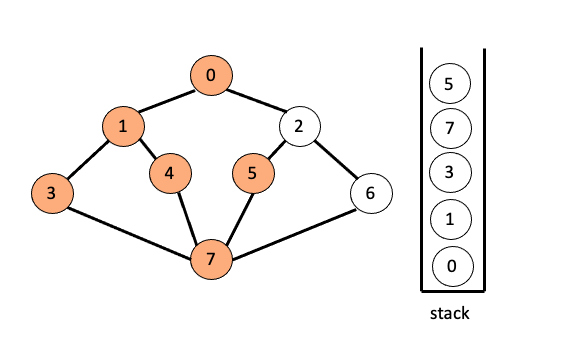
이와 같은 과정을 반복하면 2, 6 순으로 노드를 방문하게 되고 더이상 6의 인접 노드중 방문 하지 않은 노드가 없으므로 스택의 최상단 노드 6을 삭제하고, 그다음 2또한 더이상 방문하지 않은 인접 노드가 없으므로 삭제되고, 5, 7, 3, 1, 0 순으로 스택에서 삭제가 되며 마침내 스택이 비었을때 깊이 우선 탐색 알고리즘이 종료됩니다.

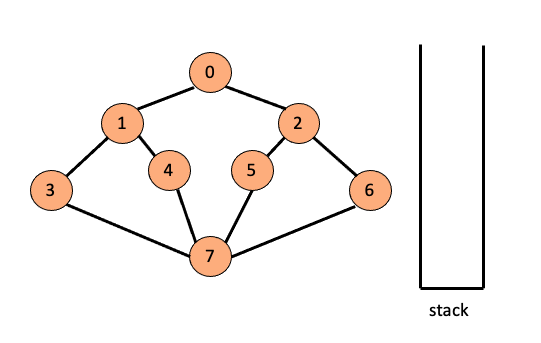
따라서 방문 경로는 0 - 1 - 3 - 7 - 4 - 5 - 2 - 6 입니다.

깊이 우선 탐색의 구현

깊이 우선 탐색 또한 그래프이기 때문에 인접 행렬 또는 인접 리스트로 구현할 수 있습니다.

void Graph::DFS()//드라이버
{
    visited = new bool[n];
    for(int i=0; i<n; i++) visited[i]=false; 
    DFS(0); //정점 0에서 탐색을 시작
    delete[] visited;
}

void Graph::DFS(const int v)
{//정점 v에서 도달 가능 하면서 아직 방문되지 않은 모든 정점들을 방문
    visited[v]=true; //방문 표시
    for(v에 인접한 각 정점 w에 대해) //그래프 표현 방법에 좌우됨
        if(!visited[w]) DFS(w); //순환호출 
}

위와 같은 DFS를 인접리스트를 사용하여 구현하였을땐 리스트 노드를 한번씩 조사해야 하므로 리스트 노드의 수 2e개에 따라 O(e) 시간이 걸리게 됩니다.

반면 인접 행렬을 사용하였다면 한 정점에 인접한 정점들을 조사하기 위해 O(n) 시간이 걸리고 전체 원소들을 조사해야 하므로 O$($n²) 시간이 걸립니다.

예제

#include<iostream>
#include<vector>
using namespace std;

vector<vector<int> > G; // 그래프의 인접 리스트 표현
vector<int> visited; // 각 정점을 방문했는지 여부를 나타낸다.

// 깊이 우선 탐색 구현
void dfs(int n, int len)
{
    if(visited[n]==0)
    {
        cout<<n<<' ';
        visited[n]=1;

        for(int i=1; i<len; i++) // 모든 인접 정점을 순회하면서
        {
            // 아직 방문한 적이 없다면 방문.
            if(G[n][i]==1 && visited[i]==0) dfs(i,len);
        }
        // 더이상 방문할 정점이 없으니, 재귀 호출을 종료하고 이전 정점으로 돌아간다.
    }
}

int main(void)
{
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);

    int v1, v2, nv, ne, search;
    cin>>nv>>ne>>search;
    G = vector<vector<int> >(nv+1, vector<int>(nv+1,0)); // nv x nv 배열
    visited = vector<int> (nv+1,0); // visited를 모두 0으로 초기화

    for(int i=0; i<ne; i++)
    {
        cin>>v1>>v2;
        G[v1][v2]=1; // 간선이 존재 한다
        G[v2][v1]=1; // 양방향 그래프 
    }

    dfs(search, nv+1);
    cout<<'\n';
    
    return 0;
}