[Algorithm] 너비 우선 탐색 BFS

너비 우선 탐색(BFS)란 시작 정점과 인접한 모든 정점을 방문한 후에 다른 정점으로 이동해 해당 정점과 인접한 모든 정점을 반복하는 것을 더 이상 방문할 정점이 없을 때 까지 반복하는 것을 말합니다.

깊이 우선 탐색을 구현하는데 스택을 사용했다면 너비 우선 탐색에는 큐(queue)가 사용됩니다.

너비 우선 탐색의 단계

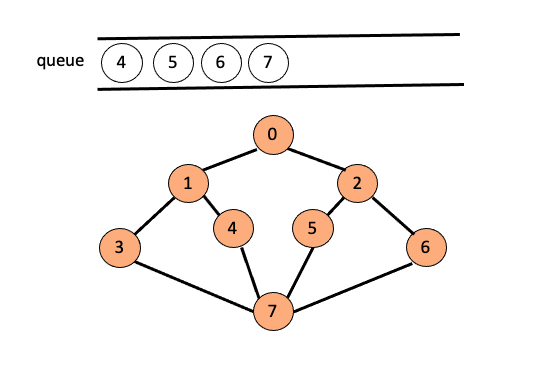
1. 시작 정점을 방문하고 큐에 삽입 합니다.

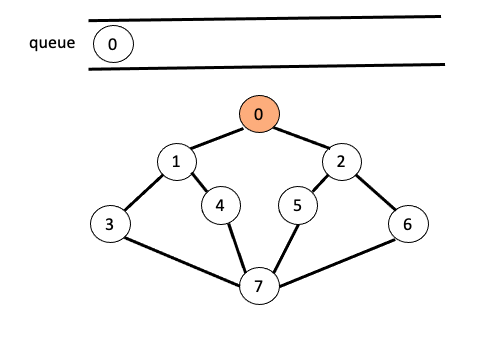
1. 큐를 pop 시키고 삭제된 node(0) 에 인접한 모든 정점을 방문하며 큐에 삽입합니다.

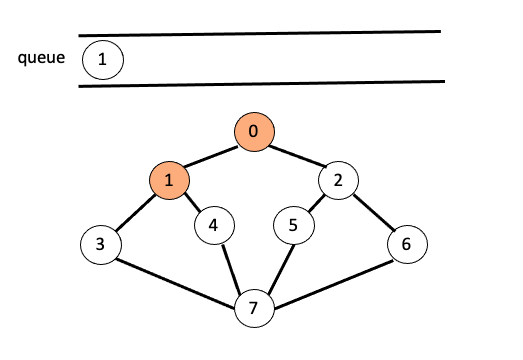
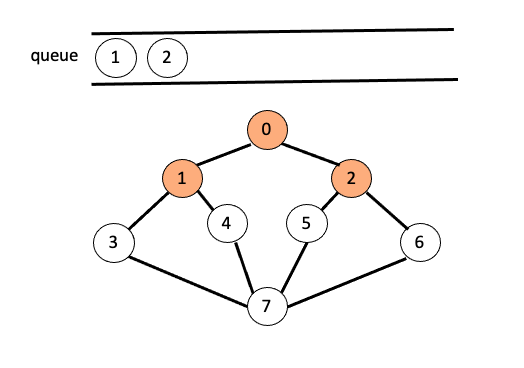
O/P : 0

1. node(0)과 인접한 모든 정점을 방문 했으면 다시 큐의 front를 pop 해주고 삭제된 node(1)에 인접한 모든 정점$($3,4)을 방문하며 큐에 삽입해 줍니다.

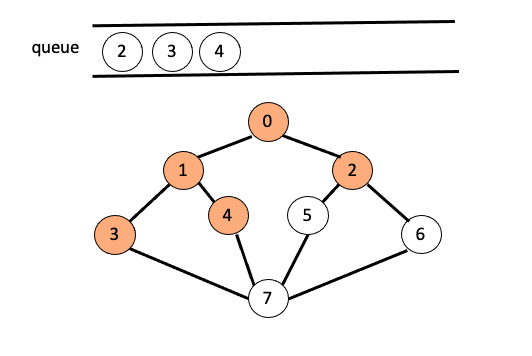
O/P : 0 - 1

1. 단계 3.을 큐가 완전히 빌때까지 반복합니다. node(1)과 인접한 모든 정점을 방문 했으므로 다시 큐의 front를 pop 해주고 삭제된 node(2)에 인접한 모든 정점 $($5,6)을 방문하며 큐에 삽입해 줍니다.

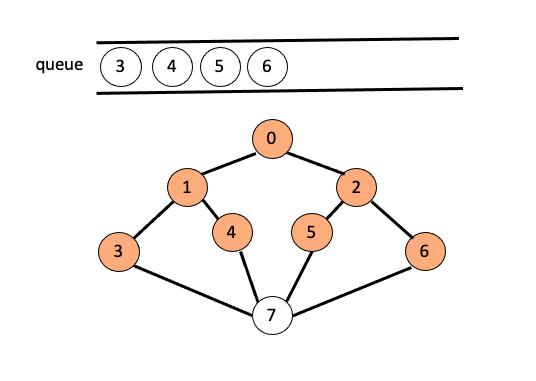
O/P : 0 - 1 - 2

1. 

O/P : 0 - 1 - 2 - 3

1. 더 이상 방문할 정점이 없으므로 큐의 front들을 출력하고 삭제하는 과정을 큐가 빌때까지 반복 합니다.

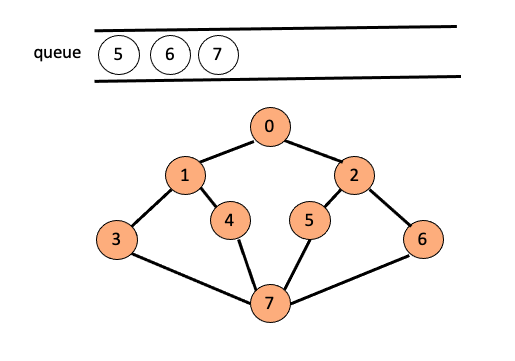
O/P : 0 - 1 - 2 - 3 - 4

. . .

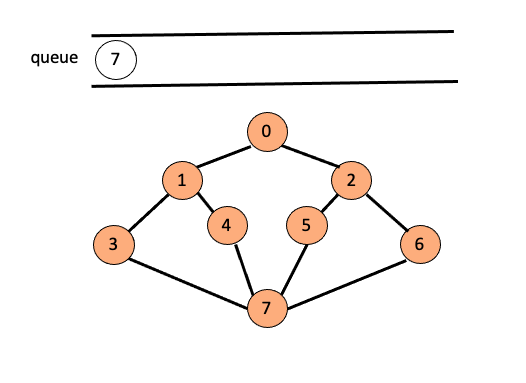
O/P : 0 - 1 - 2 - 3 - 4 - 5 - 6

1. 큐가 비었으므로 깊이 우선 탐색을 종료 합니다.

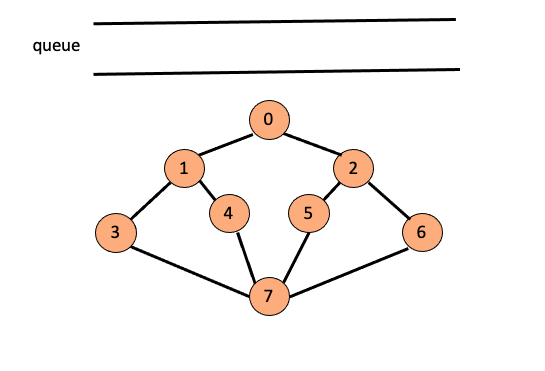
O/P : 0 - 1 - 2 - 3 - 4 - 5 - 6 - 7

너비 우선 탐색의 구현

너비 우선 탐색 또한 그래프이기 때문에 인접 행렬 또는 인접 리스트로 구현할 수 있습니다.

void Graph::BFS(int v)
{// 정점 v에서 너비 우선 탐색을 시작
    visited = new bool[n];
    for(int i=0; i<n; i++) visited[i]=false; //초기에는 정점 방문한적 없으므로
    visited[v]=true; //출발 정점 v 방문 표시
    Queue<int> q; // 구현해 놓은 Queue를 사용
    q.push(v); // 정점 v를 큐에 삽입
    while(!q.IsEmpty()) // 큐가 빌때까지 반복
    {
        v = *q.pop(v); //정점 v를 큐에서 삭제
        for(v에 인접한 모든 정점 w에 대해)
        {
            if(!visited[w])
            {
                q.push(w);
                visited[w] = true;
            }
        }
    }
    delete[] visited;
}

위와 같은 BFS를 인접리스트를 사용하여 구현하였을땐 리스트 노드를 한번씩 조사해야 하므로 리스트 노드의 수 2e개에 따라 O(e) 시간이 걸리게 됩니다.

반면 인접 행렬을 사용하였다면 한 정점에 인접한 정점들을 조사하기 위해 O(n)시간이 걸리고 전체 원소들을 조사해야 하므로 O$($n²) 시간이 걸립니다.

예제

#include<iostream>
#include<queue>
#include<vector>
using namespace std;

vector<int> visited;
vector<int> G[1001];

void BFS(int node)
{
    int u;
    queue<int> q;
    visited[node] = 1; // 해당 node 방문 처리
    q.push(node);

    while(!q.empty())
    {
        u = q.front();
        q.pop();

        // 모든 인접한 정점을 검사한다.
        for(int i=0; i < G[u].size(); i++)
        {
            int nextNode = G[u][i];
            // 처음 보는 정점이면 방문처리한다.
            if(visited[nextNode] == 0)
            {
                q.push(nextNode);
                visited[nextNode] = 1;
            }
        }
    }
}

int main(void)
{
    int n, m, start;
    int u,v;
    cin >> n >> m >> start;

    visited = vector<int> (n+1, 0);

    for(int i = 0; i < m; i++)
    {
        cin >> u >> v;
        G[u].push_back(v);
        G[v].push_back(u);
    }

    BFS(start);
    return 0;
}