[BOJ] 별찍기 - 11 C++ 풀이 [분할정복]

문제

예제를 보고 규칙을 유추한 뒤에 별을 찍어 보세요.

입력

첫째 줄에 N이 주어진다. N은 항상 3×2k 수이다. (3, 6, 12, 24, 48, …) (0 ≤ k ≤ 10, k는 정수)

출력

첫째 줄부터 N번째 줄까지 별을 출력한다.

예제 입력

24

예제 출력

                       *                        
                      * *                       
                     *****                      
                    *     *                     
                   * *   * *                    
                  ***** *****                   
                 *           *                  
                * *         * *                 
               *****       *****                
              *     *     *     *               
             * *   * *   * *   * *              
            ***** ***** ***** *****             
           *                       *            
          * *                     * *           
         *****                   *****          
        *     *                 *     *         
       * *   * *               * *   * *        
      ***** *****             ***** *****       
     *           *           *           *      
    * *         * *         * *         * *     
   *****       *****       *****       *****    
  *     *     *     *     *     *     *     *   
 * *   * *   * *   * *   * *   * *   * *   * *  
***** ***** ***** ***** ***** ***** ***** *****

접근방법

예제를 보고 특정한 패턴과 공식을 찾는것이 문제해결의 핵심이었다.

재귀를 사용하여 분할정복으로 문제를 해결하는 방식으로 접근해 보았다.

이때 분할 가능한 가장 작은단위의 삼각형은 다음과 같다.

                   *                        
                  * *                       
                 ***** 

이때 삼각형의 높이 n은 3이다.

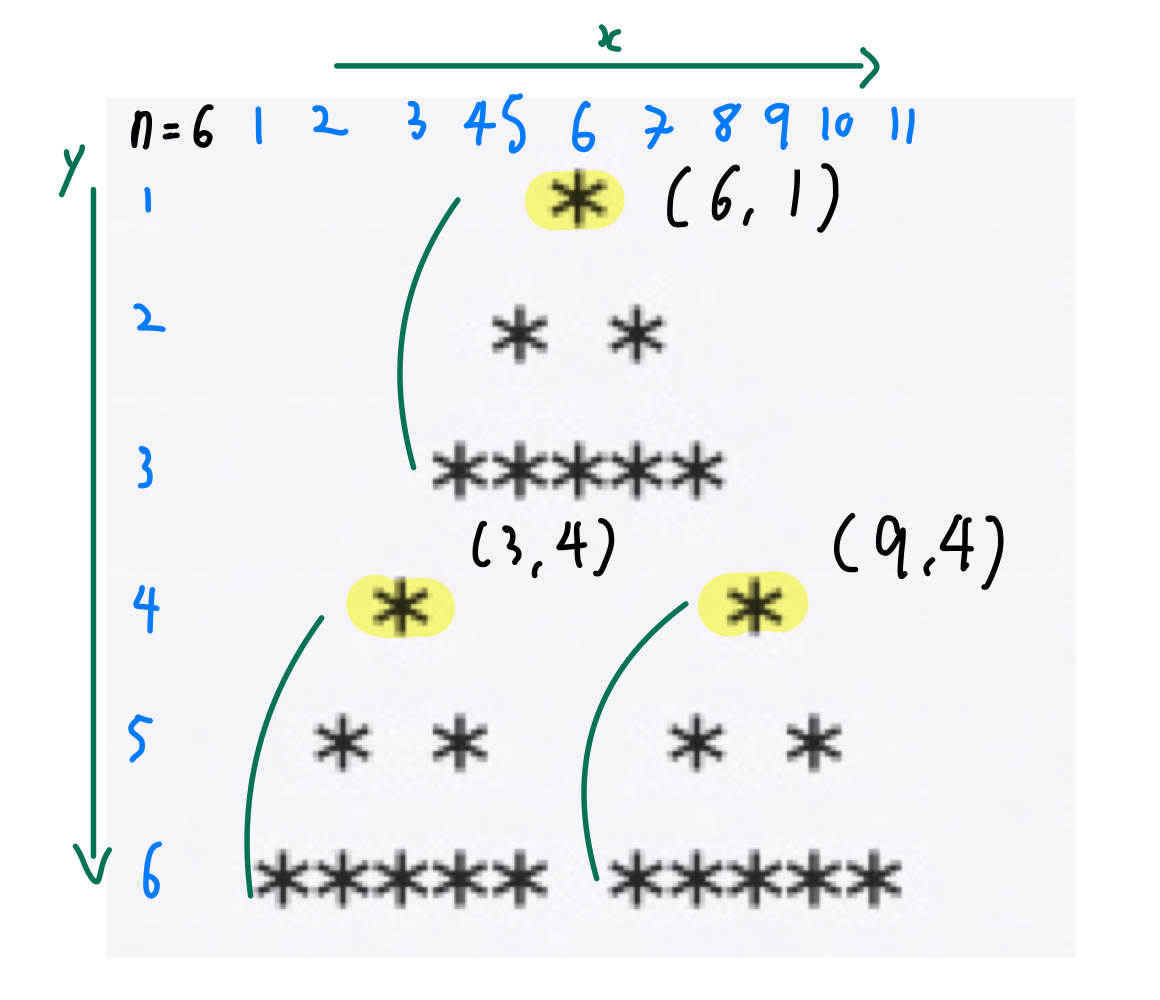
위 그림에서 n=6이며 삼각형의 시작지점을 꼭대기로 지정하였을 때, 각 삼각형의 시작지점의 위치는 다음과 같은 공식으로 나오게 된다.

(x, y)

(x/2, x-n/2, y+n/2)

(x/2, x-n/2+n, y+n/2)

해당 공식을 중심으로 재귀함수를 구현하고, 그림에서의 최대 y길이는 n, x길이는 2 x n - 1이다.

때문에 문제에서의 n의 범위에 따라 가능한 전체 그림의 x축 y축 길이를 char map[3072][6143]; 로 설정해 주었다.

구현

#include<iostream>
using namespace std;

char map[3072][6143];

void star(int n, int x, int y)
{
    // 작은 삼각형 그리기
    if(n==3)
    {
        map[y][x] = '*'; // 0,2

        map[y+1][x+1] = '*';
        map[y+1][x-1] = '*';

        map[y+2][x] = '*';
        map[y+2][x-1] = '*';
        map[y+2][x+1] = '*';
        map[y+2][x-2] = '*';
        map[y+2][x+2] = '*';
    }
    else
    {
        star(n / 2, x, y);
        star(n / 2, x-n/2, y+n/2);
        star(n / 2, x-n/2+n, y+n/2);
    }
}

int main(void)
{
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    int n;
    cin>>n;

    for(int i=0; i<n; i++)
        for(int j=0; j<2*n-1; j++)
            map[i][j] = ' ';

    star(n, n-1, 0);

    for(int i=0; i<n; i++)
    {
        for(int j=0; j<2*n-1; j++)
            cout<<map[i][j];
        
        cout<<'\n';
    }

    return 0;
}

오답노트

분할정복으로 풀어야 겠다는 생각을 하긴 했지만 도무지 공식을 유도해 내지 못하여 풀지 못한 문제였다.