[BOJ] 트리의 순회_2263 C++ 풀이

문제

n개의 정점을 갖는 이진 트리의 정점에 1부터 n까지의 번호가 중복 없이 매겨져 있다. 이와 같은 이진 트리의 인오더와 포스트오더가 주어졌을 때, 프리오더를 구하는 프로그램을 작성하시오.

접근 방법

중위 순회와 후위 순회의 특징을 파악하고 이를 활용하는 것이 중요한 문제이다.

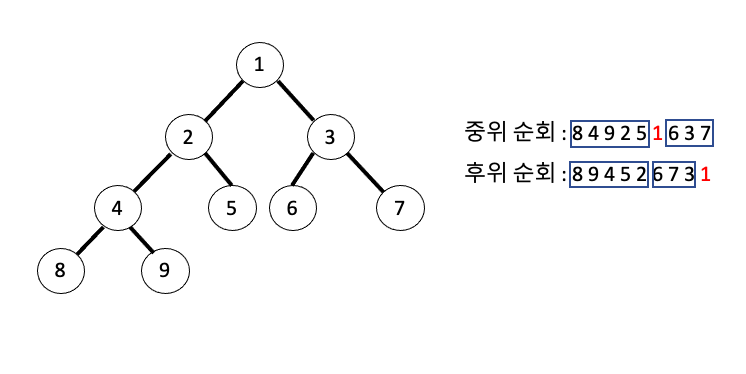
중위 순회에서 시작부분 부터 루트노드 까지가 왼쪽 서브 트리, 루트노드 이후부터 끝 부분 까지가 오른쪽 서브 트리라는 사실을 활용하여 프리 오더를 구할 수 있다.

후위 순회의 끝 값은 항상 루트 노드라는 점을 이용해 루트 노드의 값을 구하고 중위 순회 값의 index들을 저장해주는 배열을 따로 만들어서 쉽게 중위 순회에서의 root 노드의 index 값을 찾아낼 수 있다.

for(int i=0; i<n; i++)
{
        cin>>inOrder[i];
        idx[inOrder[i]] = i; // 중위 순회 값의 index들을 저장. root노드의 index값을 찾기 위해
}

int rootIdx = idx[postOrder[poEnd]]; // root의 index

찾아낸 루트 노드 값을 출력한 후 재귀를 통해 더 이상 분해할 수 없을 때 까지 트리를 분해해 가며 루트노드를 출력 해 준다.

재귀함수의 인자로는 매번 중위 순회의 시작 index, 끝 index 와 후위 순회의 시작 index, 끝 index 를 함수의 인자로 넣어주며 재귀 함수를 수행한다.

void preOrder(int inStart, int inEnd, int poStart, int poEnd) //전위 순회
{
    if(inStart > inEnd || poStart > poEnd) return;

    int rootIdx = idx[postOrder[poEnd]]; // root의 index
    int root = inOrder[rootIdx];
    int leftSize = rootIdx - inStart; //inOrder 기준 왼쪽 크기
    int rightSize = inEnd - rootIdx; // inOrder 기준 오른쪽 크기

    cout<<root<<' ';
    preOrder(inStart, rootIdx-1, poStart, poStart + leftSize - 1); //왼쪽
    preOrder(rootIdx+1, inEnd, poStart + leftSize, poEnd-1); //오른쪽
}

후위 순회에서의 왼쪽 서브트리의 끝을 알기 위해서 poStart + leftSize - 1을 해줍니다.

구현

#include<iostream>
#define Max 1000001
using namespace std;

int postOrder[Max];
int inOrder[Max];
int idx[Max];

void preOrder(int inStart, int inEnd, int poStart, int poEnd) //전위 순회
{
    if(inStart > inEnd || poStart > poEnd) return;

    int rootIdx = idx[postOrder[poEnd]]; // root의 index
    int root = inOrder[rootIdx];
    int leftSize = rootIdx - inStart; //inOrder 기준 왼쪽 크기
    int rightSize = inEnd - rootIdx; // inOrder 기준 오른쪽 크기

    cout<<root<<' ';
    preOrder(inStart, rootIdx-1, poStart, poStart + leftSize - 1); //왼쪽
    preOrder(rootIdx+1, inEnd, poStart + leftSize, poEnd-1); //오른쪽
}

int main(void)
{
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    int n;
    cin>>n;

    for(int i=0; i<n; i++)
    {
        cin>>inOrder[i];
        idx[inOrder[i]] = i; // 중위 순회 값의 index들을 저장. root노드의 index값을 찾기 위해
    }

    for(int i=0; i<n; i++) cin>>postOrder[i];

    preOrder(0, n-1, 0, n-1);
    return 0;
}

BOJ_트리의 순회